Pythonでt分布の値を出す 

t分布は母集団が正規分布していて、かつその標準偏差が未知の場合、少ない標本からもとの分布の平均値を推定するときに使われる確率分布です。
統計の教科書などの最後によく数表が載っていますが、値が結構とびとびだったりして使いにくいことがよくあります。こういうことはコンピューターにやらせた方が早くて正確な結果が得られます。
Pythonでt分布をあつかうにはscipyを使います
(注意 :Python/標準正規分布と同様の内容なので、こちらを読んでからの方が理解しやすいかも知れません。)
自由度10のt分布の横軸の値から上側確率を出すには
from scipy.stats import t t.sf(x=1.233,df=10)
結果
0.12288719525159397
とします。xが横軸の値、dfが自由度です。
自由度10のt分布の横軸の値から下側確率を出すには
from scipy.stats import t t.cdf(x=1.233,df=10)
結果
0.877112804748406
確率の定義から、この二つを加えると1となります。
t.sf(x=1.233,df=10) + t.cdf(x=1.233,df=10)
結果
1.0
よって、両方覚えなくてもどちからだけ知っておけば十分です。ただし、1から引くと精度は少しだけ落ちることがあるようなので、非常に細かい精度を問題にするなら上側確率や下側確率を直接求めた方が無難です。
累積確率から横軸の値を出すには
t.ppf(q=0.9,df=10)
結果
1.3721836411102866
とします。
上側確率から横軸の値を出すには、
t.isf(q=0.9,df=10)
結果
-1.3721836411102866
とします。
t分布の性質より、これらは符号が反転します。 よってどちらか覚えれば十分です。
正規分布と比べてみる 

t分布は自由度、つまり標本の数が多くなると正規分布に近づくとされています。
そのため、通常は標本の数が多いときは正規分布を使い、少ないときにしかt分布は使いません。
この「少ない」の具体的な数は、要求され精度によって異なるでしょうが、私の手持ちの書籍などによるとだいたい25〜30未満を意味するようです。
では、実際に自由度によってどの程度の差が出るのかをPythonで計算して、この値の妥当性を見てみます。
実際によく使いそうな確率0.95の横軸の値の比を計算してみると以下のようになりました。
- df=10
t.isf(q=0.95,df=10) / norm.isf(q=0.95)
結果
1.1018981221872615
- df=20
t.isf(q=0.95,df=20) / norm.isf(q=0.95)
結果
1.0485542389065539
以下同様にして
- df=25
1.038475845670062
- df=30
1.031861356263898
- df=100
1.0093508011061045
自由度10では10パーセントあった差が、自由度25〜30で差は3〜4パーセントになります。
自由度100あたりでようやく1パーセントを切ります。
自由度が10から30へ変化したときの減少幅の方が30から100までの減少幅よりはるかに大きく、30前後を自由度の区切りと考えるのが自然そうに思えます。
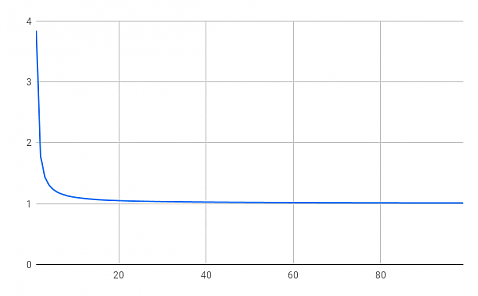
実際、上の計算を自由度1〜100まで行ってグラフにすると以下のようになりました。
25〜30程度までは差が大きく減少し、その後はほぼ横ばいになることが分かります。
| ぺージ情報 | |
|---|---|
| ぺージ名 : | Python/t分布 |
| ページ別名 : | 未設定 |
| ページ作成 : | njf |
| 閲覧可 | |
| グループ : | すべての訪問者 |
| ユーザー : | すべての訪問者 |
| 編集可 | |
| グループ : | すべての訪問者 |
| ユーザー : | すべての訪問者 |