はじめに  [1]
[1]
 [2]
[2]
Pythonでは正規分布(ガウス分布)に従う乱数を発生させる方法が標準で提供されています。
普通の一様な乱数よりは使用頻度は低いものの、正規分布は誤差などで自然に現れる確率分布で、統計の分野では非常に重要な分布です。
そのため、統計関係のテストデータの作成などにこの機能が使えます。
また、グラフィックなどで自然な形で集中したランダムな点を描画したい時や、ゲームで弾の照準に誤差を入れたいときなどにも使えます。
自分で実装するのもそう難しくはないのですが、少し面倒なので標準で使えるのは便利です。
注意:Pythonの正規分布の上側確率などを求める方法はPython/標準正規分布[3]で紹介しています。
random.gauss  [4]
[4]
 [5]
[5]
生成するにはrandom.gaussを使います。 例えば、標準正規分布に従う乱数を生成するには以下のようにします。
import random print(random.gauss(0,1))
結果:
-1.5001413318395698
など。
第一引数が平均値で第二引数が標準偏差です。
他にほぼ同様のメソッドとしてrandom.normalvariateがあります。
使い方も全く同じで第一引数が平均値で第二引数が標準偏差です。
ただし、gaussの方が高速で動作します。normalvariateはスレッドセーフのようです。(検証はしていません。)
一つだけ生成しても実際に正規分布になっているかどうか分からないので、100,000個の乱数を生成して小数第二位で四捨五入し、度数を数える以下のようなプログラムを作ってみました。
import random
dataCnt = {}
for i in range(100000):
d = round(random.gauss(0,1),1)
if d in dataCnt:
dataCnt[d] += 1
else:
dataCnt[d] = 1
sortedData = sorted(dataCnt.items())
for k in sortedData:
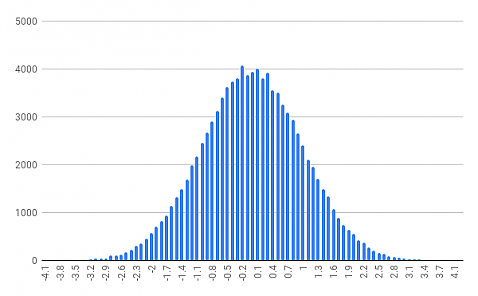
print("%.2f\t%d" % (k[0],k[1]))この結果を表計算ソフトに貼り付けてグラフを描くと次のようになりました。
乱数なので少しばらつきがありますが、ほぼ正規分布になっていることが分かります。
Pythonにはこれ以外にも、対数分布、ガンマ分布やパレート分布、ワイブル分布などが標準で実装されています。
詳しくはこちらのドキュメント[7]で。
おまけ:中心極限定理と一様分布から標準正規分布に従うランダムな数を生成する  [8]
[8]
 [9]
[9]
計算コストが高くて実用性はないのですが、一様分布と中心極限定理から標準正規分布に従うランダムな数を生成してみます。
中心極限定理とは、母集団の分布が何であれそこから抽出された無作為標本の平均値は正規分布に従い、平均値は母集団と同じになり、標本の分散は母集団の分散の標本の大きさの平方根分の一となるというものです。
そこで、たいていのプログラミング言語に実装されているランダムな一様分布を使って標準正規分布を導くことを考えてみます。
区間(a,b)の一様分布の平均は(b-a)/2、分散は(b-a)^2/12と分かっていますから、これと中心極限定理を使います。nを標本の大きさとして、平均0、分散1の標準正規分布となるようにa,bについての連立方程式を解くと、a=b=sqrt(3n)と求まります。
nを100として、標準正規分布に従うランダムな数を返す関数を作ると以下のようになります。
def cltRandom():
n = 100
sqr3 = 2 * math.sqrt(3*n)
x = 0
for i in range(n):
x += (random.random() - 0.5) * sqr3
return x / nこれを前節と同じように100,000回実行して小数第二位で四捨五入し、度数を数えてグラフを描くと以下のようになりました。
前節のグラフとほぼ同じになり、予想通り標準正規分布に従っていることが分かります。
この関数は、100回も乱数を生成するので実行速度はかなり遅く実用性はありません。
しかし、中心極限定理を実際に確かめられる簡単な例となっており、統計での正規分布の重要性を理解できると思います。
Links list
(This host) = https://njf.jp
- (This host)/cms/modules/xpwiki/?Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B#w162d0c4
- (This host)/cms/modules/xpwiki/?cmd=edit&page=Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B¶id=w162d0c4
- (This host)/cms/modules/xpwiki/?Python%2F%E6%A8%99%E6%BA%96%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83
- (This host)/cms/modules/xpwiki/?Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B#y3cda487
- (This host)/cms/modules/xpwiki/?cmd=edit&page=Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B¶id=y3cda487
- (This host)/cms/modules/xpwiki/gate.php?way=ref&_nodos&_noumb&page=Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B&src=chart.png
- https://docs.python.org/ja/3/library/random.html
- (This host)/cms/modules/xpwiki/?Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B#ue41f4eb
- (This host)/cms/modules/xpwiki/?cmd=edit&page=Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B¶id=ue41f4eb
- https://ja.wikipedia.org/wiki/%E4%B8%AD%E5%BF%83%E6%A5%B5%E9%99%90%E5%AE%9A%E7%90%86
- (This host)/cms/modules/xpwiki/gate.php?way=ref&_nodos&_noumb&page=Python%2F%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%81%86%E4%B9%B1%E6%95%B0%E3%82%92%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B&src=chartClt.png
![[PukiWiki] [PukiWiki]](https://njf.jp/cms/modules/xpwiki/image/pukiwiki.png)
 [6]
[6]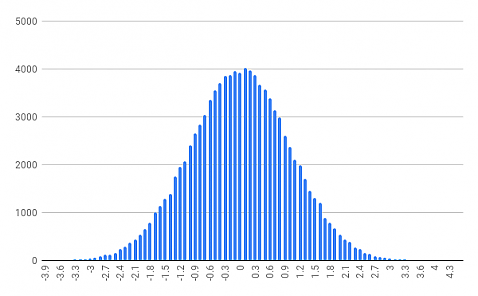 [11]
[11]